ITエンジニア基礎（アプリ開発系・インフラ系共通）

はじめに

お疲れ様です。こちらのトピックでは、ITの技術を学ぶにあたり、最低限必要な、基礎知識を 書き溜めていきます。
一気に作成できないので 少しずつ進めていきます。
おそらくこれを最初に見てから他のトピックを見れば少し理解が深まるんじゃないかなと思います。
基本知識なので インフラエンジニア やアプリケーションプログラマーなど共通の項目ですので ちょっと目を通していただけますと嬉しいです。

コンピュータで使う単位

ビット・バイト

まず一番 基本となるのがデータの単位 なのですが、一般的にはビットやバイトを使うことが多いです。他も色々ありますけれど。。。
ビットはコンピューターが扱うデータの最小単位となります。1ビットは0か1のいずれかの値を表します。
また、バイトとは8つのビットの集まりです。バイトは1ビットが8個集まって 1バイトになります。
前述したように 1ビットは2つの状態であります、0または1で表せるので1バイトでは2の8乗 通りの256通りの状態を示すことができます。

何となくわかりましたでしょうか？
10101101の様な0と1の並びをビット列やビットパターンと言います。コンピュータを学ぶ上で2進数、8進数、16進数は、普通に出てくるので
ここは押さえておきたいところです。

データの単位

データの単位ですが、よく耳にすると思いますが、ギガバイトとかギガビットとかよく携帯ショップの記憶領域容量など表現していると思います。
キロやギガやテラの単位にビットとかバイトとかがくっつき表現します。

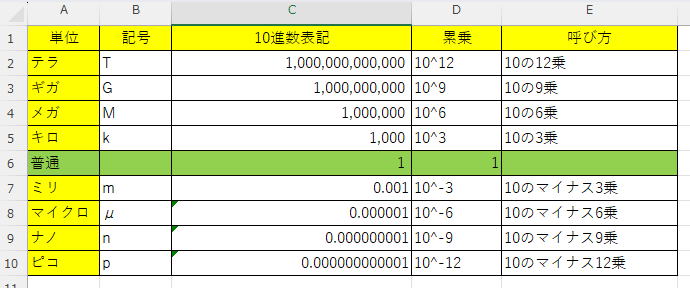＋1000倍もしくは－1000倍ごとに単位が変わります。

２進数と１０進数と１６進数

コンピュータの世界では、２進数、１０進数、１６進数がよく使われます。
数値の表現方法にはいくつかの進数（基数）があります。
2進数（Binary）、10進数（Decimal）、16進数（Hexadecimal）は、特に重要です。
1. 2進数（Binary）
基数　2
使用する数字　0, 1
特徴　コンピュータの内部処理で使われる最も基本的な数値表現。電子回路がオン（1）・オフ（0）の
状態で動作するため、コンピュータは2進数でデータを扱います。
例　10進数の 5 は 2進数で 101
　　10進数の 13 は 2進数で 1101
2. 10進数（Decimal）
基数　10
使用する数字　0, 1, 2, 3, 4, 5, 6, 7, 8, 9
特徴　一般日常的に使用する数値表現。それぞれの位は 10 の累乗として表される。（１の位は10^0、10の位は10^1　みたいな感じ）
　　　日常は、下記の計算ではなく感覚でわかっていますが、分解すると下記になります。
例　348 は 3 × 10^2 + 4 × 10^1 + 8 × 10^0
　　1024 は 1 × 10^3 + 0 × 10^2 + 2 × 10^1 + 4 × 10^0
3. 16進数（Hexadecimal）
基数　16
使用する数字　0〜9, A〜F（A=10, B=11, C=12, D=13, E=14, F=15）
特徴　コンピュータのメモリアドレスやカラーコード、機械語などで頻繁に使われる。2進数を4桁ずつ区切って表現できるため、
　　　よりコンパクトに記述可能であります。
例　10進数の 255 は 16進数で FF
　　10進数の 4096 は 16進数で 1000

それぞれの進数は、用途に応じて使い分けられます。特にプログラミングやITシステムに関わる場面では、2進数と16進数の知識が
重要になりますね。
とりあえず、へぇ～そうなんだーの温度感で覚えてくださいませ。各進数（基数）の変換については、後述します。

基数変換と桁の重みについて

基数
基数とは 桁上がりの基準となる数となります。10進数は10になる時に 桁が上がるので 10進数の基数は10となります。
同じように 2進数の基数は2、16進数の基数は、16となります。

桁の重み
基数変換を行うには桁の重みを理解しておく必要があります。
桁の重みとは 位のことです 10進数では小数点の左から順に1の位 10の位 100の位 と呼ばれています。
小数点の以下は1/10、1/100、1/1000と言うようにどんどん小さくなります。
要は 小数点第1位が1/10、小数点第2位が1/100、小数点第3位が1/1000、ということになります。
桁の重みは数が大きくなればなるほど 桁数が多くなるため 読みづらくなりますので、指数を使って解決します。
指数は数を掛け合わせる回数を表す数となります。例えば1000は、10×10×10でありますので 10の3乗となります。
表し方は、10^3となります。コンピューターの世界では この指数を使うのが一般的になりますので是非 覚えておいてくださいね。(^^)

基数変換　2進数から10進数

2進数の桁の重みは2進数の基数である2の累乗であります。
10進数 や 16進数とは 桁の重みが違うので そこは注意しましょう！
2進数から10進数へ奇数変換する際は 各桁の重みをかけてから 各桁の積を合計します。なんかちょっとわかりずらいですね！
もう少し説明すると 2進数から10進数への変換は 各桁の重みを使って計算します。各桁が2の累乗 に対応していて
それぞれの桁の数値をその累乗値と掛け合わせて最終的に合計することで 10進数へと変換されます。
例えば、2進数である　1101　を10進数に変換する場合、各桁の値を対応する2の累乗と掛け合わせます。
左から順に桁の重みを確認すると、
一番左の 1 は 2^8（8の位） に対応し、計算すると 1×8 = 8
次の 1 は 2^2（4の位） に対応し、計算すると 1×4 = 4
次の 0 は 2^1（2の位） に対応しますが、 0 があるので 0×2 = 0
最後の 1 は 2^0（1の位） に対応し、計算すると 1×1 = 1

これらを合計すると、 8 + 4 + 0 + 1 = 13 となり、2進数の1101 = 13（10進数） という結果になります。
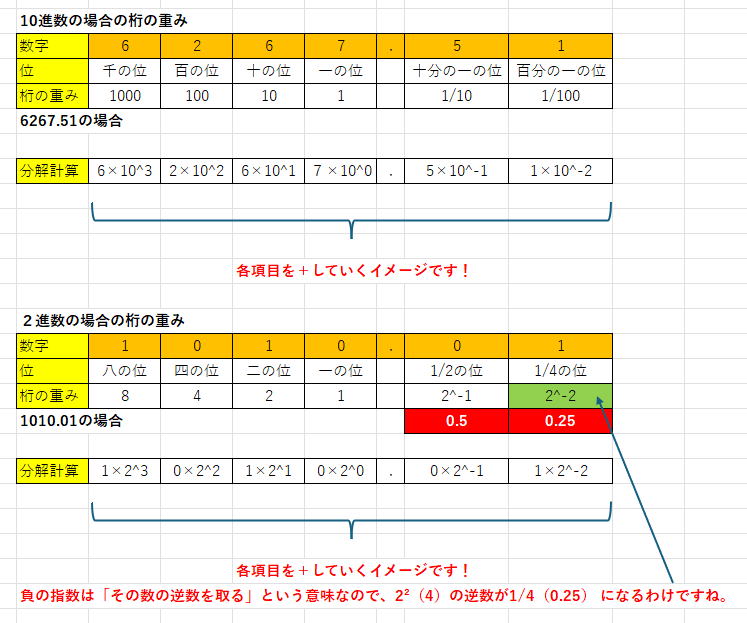
小数が含まれる場合も同様に計算できます。例えば、2進数　101.01　の場合は以下。
整数部分 101 は (1×2^2) + (0×2^1) + (1×2^0) = 4 + 0 + 1 = 5
小数部分 .01 は (0×2^-1) + (1×2^-2) = 0 + 0.25 = 0.25

これらを合計すると、2進数の　101.01 = 　5.25（10進数） となります。
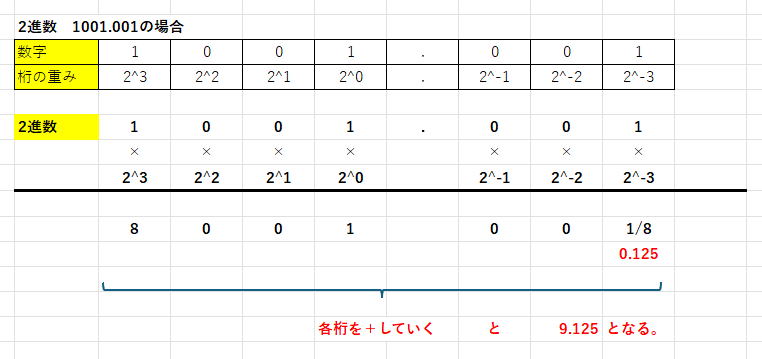
このように、各桁の値を2の累乗の重みと掛け合わせ、合計することで2進数から10進数に変換できますよ。

プログラミングの際や、Linuxコマンドで変換することができますが、仕組みの理解は必要と思います。
2進数から10進数の変換は、よく使うので必須です！

なんとなく理解できましたでしょうか。

基数変換　2進数から16進数

基数変換　10進数から2進数

10進数を2進数に変換する場合は整数部分と少数部分に分けて計算します。
例えば10進数の4.625を2進数に変換するには次のように計算します。

整数部分の計算と小数点以下の計算

10進数の数を2進数の基数2で割り算して、商が0になるまで計算を行います。
そしてあまりを逆に並べ替えます 例えば10進数の4を2進数に変換するには次のようになります。
また 小数部分の計算は10進数の小数の数に2進数の奇数 2をかけます、積のうち 整数部だけを取り出して
残った 小数部にさらに2をかける感じです。

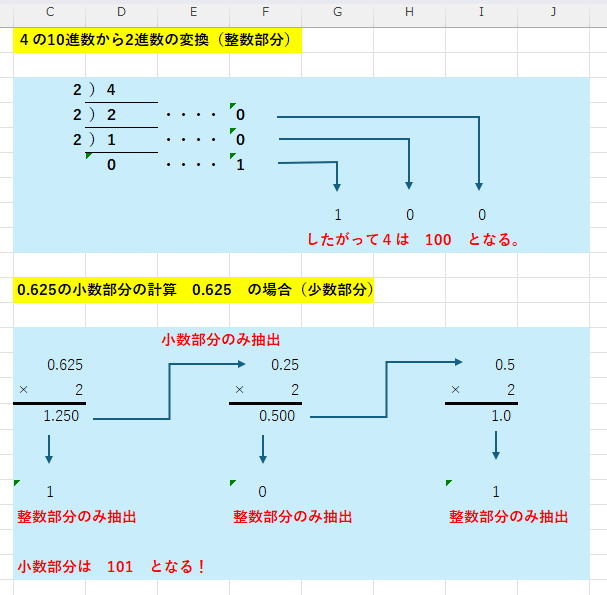上記の計算から10進数の4.625は2進数で言うと 100.101　ということになります。
割と分かりやすく説明したつもりなんですけど、理解ができなかった人は再度もう1回 読み直してください 多分わかると思います。
<重要>
上記の計算では10進数の小数から2進数の小数の変換において最終的には少数部が0になったため 計算が完了しましたが
10進数 小数から2進数 小数の変換ではほとんどの場合 小数部が0になりません。
そのため 10進数 少数を2進数 少数に変換すると大抵 無限小数になります。この場合どこかで丸めることになりますが こ
れはその時と場合でどの桁で丸めるかは 状況次第になります。

有限小数・無限小数・循環小数について

有限小数・無限小数・循環小数は、小数の種類を分類する際に重要です。
1. 有限小数
有限小数とは、小数部分が有限の桁数で終わるものです。
要は今回のように、ある時点で小数部分が終了し、それ以上続かないという特徴がです。
例））
0.75（小数第2位で終わる）
12.5（小数第1位で終わる）
3.142（小数第3位で終わる）
有限小数は、分母が2または5の累乗で表される分数として表現できます。
例））0.75 = 3/4 のように分数の形に直せるものが多いです。

2. 無限小数
無限小数とは、小数部分が途切れずに無限に続くものです。
ただし、無限小数にはさらに循環小数と非循環小数の2種類があります。
例））
0.333333…（1/3、無限に続く循環小数）
0.14159265358979…（円周率π、循環しない無限小数）
無限小数は必ずしも規則的なパターンを持つわけではなく、循環する場合もあれば、
完全に異なる数字が続く場合もあるんです。

3. 循環小数
循環小数とは、小数部分が一定のパターンで繰り返すものです。
無限小数の中でも、特定の数字が規則的に繰り返されるものがこれに分類されます。
例））
0.66666…（2/3 → 「6」が繰り返される）
0.142857142857…（1/7 → 「142857」が繰り返される）

基数変換　10進数から16進数

10進数から16進数に変換する際の基本的な手順は10進数から2進数の場合と同じです。
整数部と小数部を分けて計算します。基本 同じなので 以下のことを ポイントとして計算してみてください。

整数部
①　まず 整数部と小数部を分けます。
②　整数部から変換します。
③　10進数を16進数に変換するにはまず10進数を16進数の基数の16で割り算をして
　　商が0になるまで計算を行います。
④　16進数は前回で表に出したように、0123456789ABCDEFです。計算上 あまりが11 だったら B、13 だったらＤ、
　　という具合になります。10から15の数をアルファベットの A から F に置き換える必要があるので
　　そこは注意してください。

ちなみに 10進数の701は16進数では 2BD になります。ちょっと計算してみて！

小数部
①　まず 整数部と小数部を分けます。
②　小数部を変換します。
③　10進数の小数部分を16進数に変換するには、16を掛けて整数部分を取得するという手順を繰り返すことで
　　行います。これは、2進数の変換で2を掛ける方法と同じ原理です。

ちなみに10進数の 0.625 は16進数では　0.A となります。これも計算してみて！

念のため変換の流れ
10進数の 0.625 を16進数に変換する
①　0.625 × 16 = 10.0　　→　　 整数部分　A　（16進数では 10 = A）
②　小数部分が0になったので終了
結果： 0.625 = 0.A

例２））
10進数の 0.626 を16進数に変換する手順を説明する。（どんどん細かくなるパタン）
変換手順
①　0.626 × 16 = 10.016
　　→ 整数部分　A（16進数では 10 = A） → 小数部分　0.016　を次に計算
②　0.016 × 16 = 0.256
　　→ 整数部分　0（16進数では 0） → 小数部分　0.256　を次に計算
③　0.256 × 16 = 4.096
　　→ 整数部分　4　（16進数では 4） → 小数部分　0.096　を次に計算
④　0.096 × 16 = 1.536
　　→ 整数部分　1（16進数では 1） → 小数部分　0.536　を次に計算
⑤　0.536 × 16 = 8.576
　　→ 整数部分　8（16進数では 8） → 小数部分　0.576　を次に計算　　　（以下、継続可能）

変換結果
10進数の　0.626 　≒　 0.A0418…　（続けるとさらに細かくなります）
小数の変換は必要な精度まで続けることができ、循環する場合あるね！どこかで丸める必要がありますが
そこは、どこまでなのかは、場合によります！

n進数から10進数への変換について

これまで コンピューターで使う 2進数 や 10進数または 16進数といった代表的なところを説明してきました。
その他にも発信数や11進数 60進数などもあります。全ての変換方法を解説するわけではなく n進数というように 汎用的な変換方法を
覚えておきましょう！nには、それぞれの 基数が、入ります。
※まぁ、2進数　8進数　16進数位を覚えておけば問題ないかなと思います。念のためn進数変換です。

大丈夫だったでしょうか。基数変換は、プログラミングにも出てきますし ネットワーク 系やインフラ系にも出てきます。
基本中の基本なので覚えておいて損なしです。なんかわからなくても何回か読んでいただければ多分 理解できると思いますし、チャット GPT とか
コパイロットとかに聞いてみると もう少し理解が深まるのかもしれません。とりあえず基数変換に関してはここまでですかね！
お疲れ様でした！